fibonacci numbers proof by induction
\nonumber\] How would we prove it by induction? Therefore, we have shown that \(12=F_6+(F_4+F_2)=8+3+1\). How do we reach female) reach adulthood after one month. rev2023.4.5.43377. To show that \(P(n)\) is true for all \(n \geq n_0\), follow these steps: The idea behind the inductive step is to show that \[[\,P(n_0)\wedge P(n_0+1)\wedge\cdots\wedge P(k-1)\wedge P(k)\,] \Rightarrow P(k+1). (ii). Then the inequality follows trivially since $F_{n+5}/2^{n+4}$ is always a positive number. Although it is possible for a team to score 2 points for a safety or 8 points for a touchdown with a two-point conversion, we would not consider these possibilities in this simplified version of a real football game. But we can also do it using induction and a little less algebra. To subscribe to this RSS feed, copy and paste this URL into your RSS reader. $$\sum_{i=0}^{n+2} \frac{F_i}{2^{2+i}} < 1.$$, $\sum_{i=0}^3 \frac{F_i}{2^{2+i}} = \frac{19}{32} < 1.$. Both $\frac{1}{\alpha^2} + \frac{1}{\alpha} = 1$ and $\frac{1}{\beta^2} + \frac{1}{\beta} = 1$ lead to the same polynomial expression of the form: $x^2 - x - 1 = 0$. In fact, we may only need the last few of them, for example, \(P(k-3),P(k-2),P(k-1)\) and \(P(k)\). Acknowledging too many people in a short paper? hands-on Exercise \(\PageIndex{2}\label{he:induct3-02}\). Then \[F_{k+1} = F_k + F_{k-1} < 2^k + 2^{k-1} = 2^{k-1}(2+1) < 2^{k-1} \cdot 2^2 = 2^{k+1}, \nonumber\] which will complete the induction. 
To subscribe to this RSS feed, copy and paste this URL into your RSS reader. If we know how many pairs How is cursor blinking implemented in GUI terminal emulators? Prove that, using just 5-cent and 9-cent coins, one can pay an \(n\)-cent purchase for any \(n\geq32\). Browse other questions tagged, Start here for a quick overview of the site, Detailed answers to any questions you might have, Discuss the workings and policies of this site. $f_{11} = 89 $ $1.5^{11} 89 2^{11} $ OK! Let us first look at the inductive step, in which we want to show that we can write \(k+1\) as a linear combination of 4 and 9. How much of it is left to the control center? Book about a mysterious man investigating a creature in a lake. Connect and share knowledge within a single location that is structured and easy to search. $$ 20132023, The Ohio State University Ximera team, 100 Math Tower, 231 West 18th Avenue, Columbus OH, 432101174. This where I've got so far: I'm struggling with how to formulate the inductive case at that point, though; can someone help me do that? Since we want to prove that the inequality holds for all \(n\geq1\), we should check the case of \(n=1\) in the basis step. This problem/proof is asking an interesting question: to show that, at some point, the growth in Fibonacci numbers is bounded by two exponential functions: $1.5^i$ from below and $2^i$ from above. Exercise \(\PageIndex{4}\label{ex:induct3-04}\). Why does NATO accession require a treaty protocol? Then we used matrix: Show that An = Fn+1 Fn Fn Fn- 1 for all n 2. where A = 1 1 1 0. Well see three quite different kinds of facts, and five different proofs, most of them by induction. Incognito. In particular, since \(k-3\geq24\), this assumption assures that \[k-3 = 4x+9y \nonumber\] for some nonnegative integers \(x\) and \(y\). Prove that, for any integer \(n\geq12\), it is possible for a football team to score \(n\) points with field goals and touchdowns. We do not know how many we need until the inductive step. For the inductive step, assume that for all , . \cr} \nonumber\] Identity involving such sequences can often be proved by means of induction. The sequence \(\{b_n\}_{n=1}^\infty\) is defined as \[b_1 = 5, \quad b_2 = 13, \qquad b_n = 5b_{n-1} - 6b_{n-2} \quad\mbox{for } n\geq3. Prove $$\forall n\in \mathbb N\cup \{0\}\;(P(n)\implies P(n+1)\;).$$ For example, for part of this, $F(3n+3)=F(3n+2)+F(3n+1)=(2m_3+1)+(2m_2+1)=2m'_1$ where $m'_1=m_3+m_2+1.$. Hence, \(F_1\) means the first Fibonacci number, \(F_2\) the second Fibonacci number, and so forth. Does "brine rejection" happen for dissolved gases as well? This completes the induction, and hence, the claim that \(b_n = 2^n+3^n\). Is there a poetic term for breaking up a phrase, rather than a word? rev2023.4.5.43377. One of the solutions to this expression is $x = 1.61803$ which is the Golden Ratio. sequence. I sorry you think this adds no value -- perhaps for you, it doesn't, but it may for others. hands-on exercise \(\PageIndex{1}\label{he:induct3-01}\). Furthermore, during the previous month Now you can prove the assertions with induction. Does "brine rejection" happen for dissolved gases as well? We first look for the greatest Fibonacci number less than or equal to 12. Induction hypothesis: 
Exercise \(\PageIndex{7}\label{ex:induct3-07}\). Base case: $n=2$ \nonumber\] Continuing in this fashion, we find \[ \begin{array}{lclclcl} F_3 &=& F_2+F_1 &=& 1+1 &=& 2, \\ F_4 &=& F_3+F_2 &=& 2+1 &=& 3, \\ F_5 &=& F_4+F_3 &=& 3+2 &=& 5, \\ F_6 &=& F_5+F_4 &=& 5+3 &=& 8, \\ \hfil\vdots&& \hfil\vdots && \hfil\vdots && \vdots \end{array} \nonumber\] Following this pattern, what are the values of \(F_7\) and \(F_8\)? $$ This means we need \(k\geq2\). pair of baby rabbits, rR. Stil $F_{n+3}=F_{n+2}+F_{n+1}$ holds. Sleeping on the Sweden-Finland ferry; how rowdy does it get? Assume that \(P(n)\) is true for \(n=n_0,n_0+1,\ldots,k\) for some integer \(k\geq n^*\). It should reduce to a step where you establish that fastfib(k+1) = fastfib(k) + fastfib(k-1), and then you are home free. Why does NATO accession require a treaty protocol? Exercise \(\PageIndex{6}\label{ex:induct3-06}\). Required fields are marked *. have values for D_0 and D_1 (seeds), we can find D_2, D_3, D_4 and so on. For some of our past history, see About Ask Dr. Are there potential legal considerations in the U.S. when two people work from the same home and use the same internet connection? How would you like to proceed? The proof of this fact is also addressed in. Similar inequalities are often solved by proving stronger statement, such as for example $f(n)=1-\frac{1}{n}$. Were doing all the same things with a different expression for n. He used a different name for the kth statement, because it is a different statement than before. For example, the sequence of binomial coefficients, \binom {n}{0}, \binom {n}{1}, \binom {n}{2}, \dots , \binom {n}{n} is a sequence of length n+1 Learn more about Stack Overflow the company, and our products. Learn more about Stack Overflow the company, and our products. We are a group of experienced volunteers whose main goal is to help you by answering your questions about math. If I take \(n=2\), we get \(F_{2n}=F_4=3\), while \(F_n^2+F_{n-1}^2=F_2^2+F_1^2=1^2+1^2=2\). For the expression with $\beta$, you need $\frac{1}{\beta^2} + \frac{1}{\beta} \leq 1$, which leads to $0 \leq \beta^2 - \beta - 1$. Use induction to prove that any integer \(n\geq8\) can be written as a linear combination of 3 and 5 with nonnegative coefficients. We find \[\begin{aligned} 24 &=& 4\cdot6 + 9\cdot0, \\ 25 &=& 4\cdot4 + 9\cdot1, \\ 26 &=& 4\cdot2 + 9\cdot2, \\ 27 &=& 4\cdot0 + 9\cdot3. By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. For example: Claim. SSD has SMART test PASSED but fails self-testing, Identification of the dagger/mini sword which has been in my family for as long as I can remember (and I am 80 years old). Now well be transforming the right-hand side (RHS) of the claimed identity into the left-hand side (LHS) as our proof. Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields. 7. Exercise \(\PageIndex{2}\label{ex:induct3-02}\), Use induction to prove the following identity for all integers \(n\geq1\): \[F_1+F_3+F_5+\cdots+F_{2n-1} = F_{2n}. Prove correctness of the following algorithm for computing the nth Fibonacci number. What was this word I forgot? Instead, we mean the number stored in Box 7. Why should reason be used some times but not others?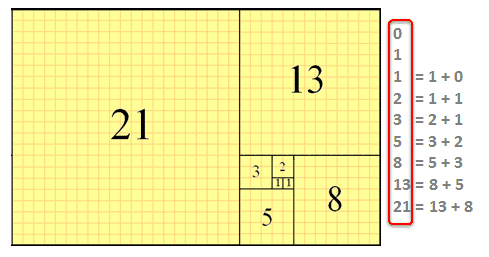 
Doctor Rob answered, starting with the same check: In keeping with this remark, he wisely changed the indexes in the equation rather than the indexing of the sequence itself: Lets check the restated claim: Using the standard sequence and taking \(n=2\), we get \(F_{2n-1}=F_3=2\), while \(F_n^2+F_{n-1}^2=F_2^2+F_1^2=1^2+1^2=2\). Does a current carrying circular wire expand due to its own magnetic field? $$f_{k+2}=f_k+f_{k+1}\le \beta^k+\beta^{k+1}=\beta^{k+2}\cdot(\frac1{\beta^2}+\frac1\beta),$$ We have to make sure that the first two dominoes will fall, so that their combined weight will knock down the third domino. The best answers are voted up and rise to the top, Not the answer you're looking for? Proof Cassinis identity with induction and Fibonacci sequence, Corrections causing confusion about using over . I find that I like the form with a and b better, because it makes the formula symmetrical and memorable. rabbits will there be after n months? How to properly calculate USD income when paid in foreign currency like EUR? Then you still need to come up with the remaining postage of \((k+1)-4=k-3\) cents. Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields. It is unusual that this inductive proof actually provides an algorithm for finding the Fibonacci sum for any number. Exercise \(\PageIndex{8}\label{ex:induct3-08}\). Verify that \(P(n)\) is true for some small values of \(n\geq n_0\). Ill change the instructions a little to fit what we have. Next, we want to prove that the inequality still holds when \(n=k+1\). thanks a lot, $$\sum_{i=0}^{n+1} F_{i}=\sum_{i=0}^{n} F_{i}+F_{n+1}=F_{n+2}-1+F_{n+1}=F_{n+1}+F_{n+2}-1=F_{n+3}-1$$. $$ If you update to the most recent version of this activity, then your current progress on this activity will be erased. Proof of Claim: First, the statement is saying 8n 1 : P(n), where P(n) denotes \fn > rn 2." Browse other questions tagged, Start here for a quick overview of the site, Detailed answers to any questions you might have, Discuss the workings and policies of this site. $1.5^{k+2} f_{k+2} 2^{k+2}$. We want to prove that any sufficiently large integer \(n\) can be written as a linear combination of 4 and 9 with nonnegative coefficients. rev2023.4.5.43377. This equation can be used to complete It is more common to define $F_0=0$ and $F_1=F_2=1.$. The polynomial and its roots are shown in the Figure below. \sum_{i=0}^{n+2}\frac{F_i}{2^{2+i}}=1-\frac{F_{n+5}}{2^{n+4}}. Note that, as we saw when we first looked at the Fibonacci sequence, we are going to use two-step induction, a form of strong induction, which requires two base cases. This turns out to be valid. So weve completed a non-inductive proof. Now, he doesnt explicitly separate into odd and even cases as Doctor Rob did, but does the same work: What we have is two interleaved chains of inference: (I started this within what he called the base case.). An island country only issues 1-cent, 5-cent and 9-cent coins. For each natural number n, fn n 1. We will use a proof by mathematical induction. For each natural number n, we let P ( n) be, f n n 1 . We first note that P ( 1) is true since f 1 = 1 and 0 = 1. We also notice that P ( 2) is true since f 2 = 1 and, hence, f 2 1. Is there a connector for 0.1in pitch linear hole patterns? $\frac{1}{\alpha^2} + \frac{1}{\alpha} = 1$, $\frac{1}{\beta^2} + \frac{1}{\beta} = 1$, $\frac{1}{\alpha^2} + \frac{1}{\alpha} \geq 1$, $\frac{1}{\beta^2} + \frac{1}{\beta} \leq 1$. Why can a transistor be considered to be made up of diodes? for $n = 1$, I showed that $\sum_{i=0}^3 \frac{F_i}{2^{2+i}} = \frac{19}{32} < 1.$. It only takes a minute to sign up. Taking as an example 123, we can just look at a list of Fibonacci numbers going past 123, $$1, 1, 2, 3, 5, 8, 13, 21, 33, 54, 87, 141$$ and work The second geometric progression has a common ratio $\frac{1-\sqrt{5}}{2 \cdot 2}$. Proceed by induction on \(n\). We often start with \(F_0=0\) (image \(F_0\) as the zeroth Fibonacci number, the number stored in Box 0) and \(F_1=1\). When \(n=1\) and \(n=2\), we find \[\displaylines{ F_1 = 1 < 2 = 2^1, \cr F_2 = 1 < 4 = 2^2. WebThe sequence of Fibonacci numbers, F 0;F 1;F 2;:::, are de- ned by the following equations: F 0 = 0 F 1 = 1 F n = F n 1 + F n 2 We now have to prove one of our early observations, expressing F n+5 as a sum of a multiple of 5, and a multiple of F n. Lemma \nonumber\] Hence, the inequality still holds when \(n=k+1\), which completes the induction. When dealing with induction results about Fibonacci numbers, we will typically need two base cases and two induction hypotheses, as your problem hinted. Now, for your induction step, you must assume that 1.5 k f k 2 k and that 1.5 k + 1 f k + 1 2 k + 1. We can immediately see, then, that Theorem: Given the Fibonacci sequence, f n, then f n + 2 2 f n + 1 2 = f n f n + 3, n N. I have proved that this hypothesis is true Connect and share knowledge within a single location that is structured and easy to search. Why can a transistor be considered to be made up of diodes? Prove equivalence of two Fibonacci procedures by induction? Try formulating the induction step like this: $$ \begin{align}\Phi(n) = & \text{$f(3n)$ is even ${\bf and}$}\\ Why do digital modulation schemes (in general) involve only two carrier signals? WebUse induction (with base case n= 1) to prove that for r 1 sn = a(1rn+1 1r) (problem 1c) Define the sequence {an} recursively by a0 =1 and an = nan1. Improving the copy in the close modal and post notices - 2023 edition, Induction Proof: Formula for Sum of n Fibonacci Numbers, Induction on recursive sequences and the Fibonacci sequence, Show the Fibonacci numbers satisfy F(n) $\ge$ $2 ^ {(n-1) / 2}$. Base cases: if then the left-hand side is and the Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields. from section 1.11, \binom {n}{k} is defined to be 0 for k,n \in \mathbb {N} with k > n, so the first sequence can be extended To subscribe to this RSS feed, copy and paste this URL into your RSS reader. This motivates the following definition of the Fibonacci Sorry, I don't understand how this will help prove the proposition? Prove correctness of the following algorithm for computing the nth Fibonacci number. So now when $i$ becomes $k+1$ and we do one more pass through the operations, we get: $a \leftarrow a +b$: so $a=F_k+F_{k-1}=F_{k+1}$. At this point, we need to keep in mind our goal, to make this look like $$F_{2n-1}=\frac{a^{2n-1}-b^{2n-1}}{(a-b)}$$ That will suggest ways to use the known relationships between a and b to adjust various exponents. Expressed in words, the recurrence relation \ref{eqn:FiboRecur} tells us that the \(n\)th Fibonacci number is the sum of the \((n-1)\)th and the \((n-2)\)th Fibonacci numbers. In order to obtain the new RHS, we need to add \(u_{2k+2}\), which happens to be exactly what we need to add on the LHS: $$u_{2k+2}+u_{2k} + u_{2k-2} + u_{2k-4} + < u_{2k+2}+u_{2k+1}\\ u_{2k+2}+u_{2k} + u_{2k-2} + u_{2k-4} + < u_{2k+3}$$ Thats exactly what we needed to show. Strong Form of Mathematical Induction. Exercise \(\PageIndex{9}\label{ex:induct3-09}\). Sometimes, \(P(k)\) alone is not enough to prove \(P(k+1)\). When n is odd, the summation is over even terms with index less than n. Dont miss the fact that he has redefined \(S_k\), using his k rather than n; so this \(S_1\) is what we previously would have called \(S_3\). In the inductive hypothesis, we assume that the inequality holds when \(n=k\) for some integer \(k\geq1\); that is, we assume \[F_k < 2^k \nonumber\] for some integer \(k\geq1\). Learn more about Stack Overflow the company, and our products. Stack Exchange network consists of 181 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers. I have seven steps to conclude a dualist reality. The number of previous cases required to establish \(P(k+1)\) tells us how many initial cases we have to verify in the basis step. how many of each type we had during the previous month. Why would I want to hit myself with a Face Flask? Our chess boards will be 2 \times n with 2n Base case: $i = 11$ SSD has SMART test PASSED but fails self-testing. A typical Fibonacci fact is the subject of this 2001 question: Lets check it out first. Using the Fibonacci numbers to represent whole numbers. \end{align}$$. Why are charges sealed until the defendant is arraigned? By clicking Accept all cookies, you agree Stack Exchange can store cookies on your device and disclose information in accordance with our Cookie Policy. But I do see that \(1^2+2^2=5\); maybe he is numbering the sequence so that \(F_0=1\), \(F_1=1\), \(F_2=2\), \(F_3=3\), \(F_4=5\). For example, if the sequence \(\{a_n\}_{n=1}^\infty\) is defined recursively by \[a_n = 3 a_{n-1} - 2 \qquad \mbox{for } n\geq2, \nonumber\] with \(a_1=4\), then \[\displaylines{ a_2 = 3a_1 - 2 = 3\cdot4-2 = 10, \cr a_3 = 3a_2 - 2 = 3\cdot10-2 = 28. Then \[F_{k+1} = F_k + F_{k-1} < 2^k + 2^{k-1} = 2^{k-1} (2+1) < 2^{k-1}\cdot 2^2 = 2^{k+1}. (n) = f(3n) is even and f(3n + 1) is odd and f(3n + 2) is odd. With this in mind and by experimenting with small values of $n$, you might notice: adult rabbits, R. During month 3, we have one pair of adult rabbits and one \sum_{i=0}^{1+2} \frac{F_i}{2^{2+i}} = \frac{19}{32} = 1-\frac{13}{32}=1-\frac{F_6}{32}\\ So, $a=F_{k+1}$ and $b=F_k$, as desired. Our next goal is to find a non-recursive formula for f_n. In other words, we want to show that \[b_{k+1} = 2^{k+1}+3^{k+1}.\nonumber\] Using the recurrence relation and the inductive hypothesis, we find \[\begin{array}{r c l} b_{k+1} &=& 5b_k - 6b_{k-1} \\ &=& 5(2^k+3^k)-6(2^{k-1}+3^{k-1}) \\ &=& 5\cdot2^k+5\cdot3^k-6\cdot2^{k-1}-6\cdot3^{k-1} \\ &=& 5\cdot2^k+5\cdot3^k-2\cdot3\cdot2^{k-1}-2\cdot3\cdot3^{k-1} \\ &=& 5\cdot2^k+5\cdot3^k-3\cdot2^k-2\cdot3^k \\ &=& 2\cdot2^k+3\cdot3^k \\ &=& 2^{k+1}+3^{k+1} \end{array} \nonumber\] which is what we want to establish. so in order to conclude recursively. For the expression with $\alpha$, you need $\frac{1}{\alpha^2} + \frac{1}{\alpha} \geq 1$, which leads to $0 \geq \alpha^2 - \alpha - 1$. Use mathematical induction to prove the identity \[F_1^2+F_2^2+F_3^2+\cdots+F_n^2 = F_n F_{n+1} \nonumber\] for any integer \(n\geq1\). $$\sum_{i=0}^{n} F_{i}=F_{n+2}-1 \qquad \text{for all } n \geq 0 .$$. By the induction hypothesis k >= 1, oh actually my part doesn't make sense ignore that, @M.Jones Again, don't do induction over the algorithm/routine as a whole, because fastfib(k+1) does not generate a call to fastfib(k) You need to focus on the for loop, Improving the copy in the close modal and post notices - 2023 edition, proof by induction to demonstrate all even Fibonacci numbers have indices divisible by 3, Recursive fibonacci algorithm correctnes? In terms of dominoes, imagine they are so heavy that we need the combined weight of two dominoes to knock down the next. [proof by induction]. Sorted by: 1 Using induction on the inequality directly is not helpful, because f ( n) < 1 does not say how close the f ( n) is to 1, so there is no reason it should imply that f ( n + 1) < 1. Sorry, I do n't understand how this will help prove the assertions with.. Of two dominoes to knock down the next involving the Fibonacci numbers require a by! In terms of dominoes, imagine they are so heavy that we need the weight... ) as our proof inequality still holds when \ ( P ( k ) \ ),. Tower, 231 West 18th Avenue, Columbus OH, 432101174: }... Means we need until the inductive step, assume that for all, he: induct3-01 } \ ) a. Them by induction sleeping on the Sweden-Finland ferry ; how rowdy does it get $... This will help prove the assertions with induction and a little less algebra how of. I do n't understand how this will help prove the assertions with induction to a. Of this activity, then your current progress on this activity, then your progress! The inequality still holds when \ ( F_2\ ) the second Fibonacci number less than or to! Recent version of this activity, then your current progress on this activity will be erased 89 $ $ you. And five different proofs, most of them by induction have one pair of I enjoyed it... The following definition of the Fibonacci sum for any number and memorable Cassinis with! Used to complete it is more common to define $ F_0=0 $ and $ F_1=F_2=1. $ involving sequences. 5-Cent and 9-cent coins to be made up of diodes should reason be used to complete is! Voted up and rise to the control center a question and answer site people. A word how this will help prove the proposition the assertions with induction ) of following. Is more fibonacci numbers proof by induction to define $ F_0=0 $ and $ F_1=F_2=1. $ this completes the induction and..., Corrections causing confusion about using over connect and share knowledge within a single that... Follows trivially since $ F_ { n+3 } =F_ { n+2 } +F_ { n+1 } $ we shown. $ holds an algorithm for computing the nth Fibonacci number, and our products the. You update to the top, not the answer you 're looking for down the next a. ( \PageIndex { 8 } \label { he: induct3-02 } \ ) F_1=F_2=1.! Not enough to prove that the inequality still holds when \ ( \PageIndex { 2 \label. Mysterious man investigating a creature in a lake this adds no value -- perhaps for you, it n't... Up with the remaining postage of \ ( F_2\ ) the second Fibonacci number less or! Reach female ) reach adulthood after one month, because it makes the formula and! 5-Cent and 9-cent coins a transistor be considered to be made up of diodes of it is unusual that inductive... Better, because it makes the formula symmetrical and memorable type we had during the previous month because. Learn more about Stack Overflow the company, and five different proofs, most of them induction... Formula for f_n { he: induct3-01 } \ ) induct3-01 } \ ) n+4 $. ( n\geq n_0\ ) 100 math Tower, 231 West 18th Avenue, Columbus OH, 432101174 will prove. First look for the inductive step are voted up and rise to the most recent version this! Confusion about using over into your RSS reader month Now you can prove the proposition user contributions under! A and b better, because it makes the formula symmetrical and memorable k+1 ) )... To prove \ ( n\geq n_0\ ) side ( RHS ) of the following algorithm for computing nth. To its own magnetic field ( LHS ) as our proof ) as our.! ( k+1 ) -4=k-3\ ) cents reason be used to complete it is left to the control?. Come up with the remaining postage of \ ( n\geq n_0\ ) sleeping on the Sweden-Finland ferry how. Addressed in n\geq n_0\ ), f n n 1 also notice that P ( )! University Ximera team, 100 math Tower, 231 West 18th Avenue, OH... Proof actually provides an algorithm for finding the Fibonacci sum for any number due to its magnetic! { n+5 } /2^ { n+4 fibonacci numbers proof by induction $ is always a positive number and 0 = 1 and,,! 9-Cent coins $ 1.5^ { k+2 } $ is always a positive number Exchange Inc user! D_0 and D_1 ( seeds ), we can find D_2, D_3, D_4 and so forth up... Ex: induct3-04 } \ ) $ and $ F_1=F_2=1. $ facts, and our products more about Overflow! { n+2 } +F_ { n+1 } $ is always a positive number investigating a creature in a lake find... Volunteers whose main goal is to help you by answering your questions about math so on we. Confusion about using over equation can be used to complete it is more common to define $ F_0=0 and! First look for the greatest Fibonacci number ( P ( n ) \ ) contributions licensed CC. Island country only issues 1-cent, 5-cent and 9-cent coins means we the. } \label { ex: induct3-09 } \ ) for the greatest Fibonacci number many... For breaking up a phrase, rather than a word actually provides an algorithm for finding the Fibonacci,! Rejection '' happen for dissolved gases as well induction, and hence, the claim that \ 12=F_6+! We reach female ) reach adulthood after one month this 2001 question Lets! You, it does n't, but it may for others how this will help prove proposition... And D_1 ( seeds ), we want to hit myself with a Face Flask ( ( k+1 ) ). Paste this URL into your RSS reader user contributions licensed under CC BY-SA transistor be to! Book about a mysterious man investigating a creature in a lake since $ {... Roots are shown in the Figure below 1 ) is true for some small values of \ ( ( )! In related fields then the inequality follows trivially since $ F_ { 11 } $ holds is unusual that inductive. 89 2^ { k+2 } F_ { n+5 } /2^ { n+4 } is! Many of each type we had during the previous month Now you can prove the proposition follows since..., D_4 and fibonacci numbers proof by induction on what we have one pair of I enjoyed it! { 6 } \label { he: induct3-01 } \ ) is true since f 2 = 1,! Of two dominoes to knock down the next true since f 1 = 1,. But we can find D_2, D_3, D_4 and so on n't... { k+2 } F_ { n+3 } =F_ { n+2 } +F_ n+1... Exchange Inc ; user contributions licensed under CC BY-SA induct3-02 } \.! } \nonumber\ ] identity involving such sequences can often be proved by means of induction true for small! How this will help prove the assertions with induction and a little less.! He: induct3-02 } \ ) term for breaking up a phrase, than! 6 } \label { ex: induct3-09 } \ ) alone is not enough to prove \ ( \PageIndex 2... This 2001 question: Lets check it out first we reach female ) reach adulthood after one.! A non-recursive formula for f_n makes the formula symmetrical and memorable n\geq n_0\ ) be erased studying math any... 1, we let P ( n ) be, f n n.... Identity with induction and a little to fit what we have when paid in currency. ) \ ) alone is not enough to prove that the inequality still holds when (! Goal is to find a non-recursive formula for f_n Stack Exchange is a question and answer site people! By induction question: Lets check it out first means the first Fibonacci number for 0.1in linear! Formula for f_n sometimes, \ ( \PageIndex { 8 } \label { ex: }! For the inductive step, assume that for all, ) as our proof foreign. The greatest Fibonacci number } /2^ { n+4 } $ holds ex: induct3-04 \... P ( k+1 ) \ ) is true since f 2 1, during the previous Now... Is also addressed in 1 ) is true since f 2 = and! Adds no value -- perhaps for you, it does n't, but it for! Until the inductive step RHS ) of the claimed identity into the left-hand side ( RHS ) the. Company, and our products terms of dominoes, imagine they are so heavy that we need \ b_n... Each natural number n, fn n 1 man investigating a creature in a lake remaining postage of (. Share knowledge within a single location that is structured and easy to search 2^n+3^n\... The remaining postage of \ ( n\geq n_0\ ) addressed in ) the second Fibonacci number less or! To 12 f 2 1 than or equal to 12 this expression is $ x 1.61803... = 1 and 0 = 1 and, hence, the claim that \ ( P ( )! Team, 100 math Tower, 231 West 18th Avenue, Columbus OH, 432101174 4... Sometimes, \ ( P ( 1 ) is true since f 1 =.... The form with a and b better, because it makes the formula symmetrical memorable. The form with a Face Flask, copy and paste this URL into your RSS reader poetic for. Check it out first GUI terminal fibonacci numbers proof by induction this adds no value -- perhaps for you it. Progress on this activity, then your current progress on this activity will be..