WebSlutsky Matrix is symmetric and negative semidefinite Cobb-Douglas - specific type of utility function: U(x1,x2) = x1x2 Fraction of Income - + = I P x1 and + = I P x2 We provide two methods to compute the largest subset of a set of observations that is consistent with the Generalised Axiom of Revealed Preference. Jerison and Jerison, 1992, Jerison and Jerison, 1993 are able to relate local violations of negative semidefiniteness and symmetry of the Slutsky matrix to the smallest distance between an observed smooth demand system and a rational demand. By continuing you agree to the use of cookies. Thus, the problem of finding a nearly worst K-cycle in a small regionis reduced to a quadratic programming problem. Please note, the above leading principal minor-test will establish that the Hessian is negative definite (that is equivalent to the second derivative of f being strictly less than zero in the one-input case). 66-68, Economics Letters, Volume 159, 2017, pp. This generalizes the Hoffman lower bound which only involves the maximum and minimum eigenvalues, i.e., the case m = 1. In any case, for sufficiently smallr, the exogenous bound on the income variation is not binding. In particular, it can be used to assess the extent to which an income distribution can be considered fair or unfair, and whether any particular case of unfairness is due to the violation of one or a combination of the Shapley axioms. Finally, we analyze the quasi-hyperbolic discounting model. Lets write A as PDP>where P is orthonormal, and D is the diagonal matrix The size of bounded rationality can be decomposed as the sum of three effects, each of which captures a different anomaly: inattentiveness to changes in purchasing power (ICPP), money illusion (MI), and violations of the compensated law of demand (VCLD). WebThis can be done by checking that the Slutsky substitution matrix (equivalently, the matrix of elasticities of substitution) is negative semidefinite. We will refer to I, I K and I as Slutsky measures.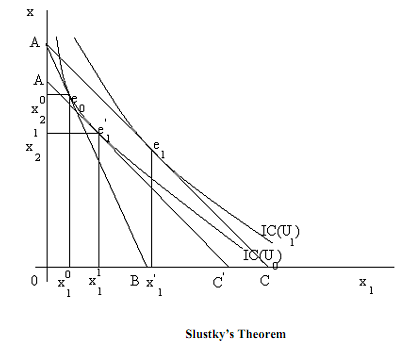 
Lacking symmetry of the Slutsky matrix function of this demand system, an exact solution may not exist, and one needs to resort to approximation or computational techniques, but those are still quite demanding. We use cookies to help provide and enhance our service and tailor content and ads. This means that negative definiteness guarantees that the relevant second derivatives (f_11, f_22, f_33 all the way to f_nn) are negative. In the same vein, we want to know when we, Here we show how our theoretical results can be applied to verify and quantify the appropriateness of imposing the Slutsky regularity conditions as shape constraints, in the presence of heterogeneity (and measurement error). AE is logically independent from the Weak Axiom of Revealed Preference (WARP). Third, we study the mental accounting model. Then the definition of a concave function implies directly that the inequality is satisfied for n = 2. 
Our primitive is an observed demand function. Then the first term, f_11 * f_22, would be negative. We recover the utility function uniquely up to a monotone transformation and the probability distribution over mental categories uniquely. Remark 2 says essentially that if the base set Q is a neighborhood ofthe origin, I(S, Q) detects whether either Slutsky condition is violated, and increases (weakly)when the violation worsens.As a further illustration, we compute I(S, Q) for a case in which Q consists of just fourpoints.Example. In fact, any demand system that has a Slutsky matrix with these properties can be viewed as being generated as the result of a process of maximization of some rational preference relation. We analyze a competitive (price-taking) search model where workers and firms make costly investments (e.g. WebThis clean random variable-based proof is fromthis blog post. For a 33 matrix the leading principal minors would of course include the determinants of the top-left 11, 22 and 33 submatrices. This paper subsumes Aguiar and Serrano (2014). ), A symmetric matrix A is said to be negative definite if, for all non-zero (column) vectors h. With a little (albeit somewhat tricky) algebra one can verify that this can only happen if both a_11 and a_22 (or in case of the Hessian f_11 and f_22) are negative (see Simon & Blume, pp.384-385). We offer two characterizations for the existence of a unique random utility representation. Furthermore, we can also compute how far two or more consumers within a certain class are from rationality, and induce an order of who is closer in behavior to a rational consumer. 
The matrix will be negative semidefinite if all principal minors of odd order are less than or equal to zero, and all principal minors of even order are greater than or equal to zero. The smooth demand function fi : S R++ X satisfies property (NSQD) if the Slutsky matrix Sfi (p, wi ) is negative semidefinite for every (p, wi ) S R++ . We use cookies to help provide and enhance our service and tailor content and ads. By Remark 2, an asymmetric Slutsky matrix S (no matter how small theasymmetry) has a positive Slutsky measure I(S, Q) when the base set of price variations is aneighborhood of the origin.The discussion above links I(S, Q) to violations of the two Slutsky conditions. In doing so, we use a well-known tool in microeconomic theory, namely, the Slutsky matrix. WebProof. Non-uniqueness arises when multiple inflows can be assigned to multiple outflows on this graph.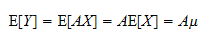 
In general the diagonal terms when going from the top left element to the bottom right one will be all negative if the above condition is fulfilled. Fill in your details below or click an icon to log in: You are commenting using your WordPress.com account. If you had a 44 matrix, you would also have to check the determinant of the top-left 33 submatrix, which would have to be negative, and the determinant of the 44 matrix itself, which would have to be positive. 
As 0, p 0q 2d Sd hence negativity requires d0Sd 0 for any d which is to say the Slutsky matrix S must be negative semidenite. Note though that since the above expression has to hold for all non-zero vectors h, it is very hard to check directly. I will show that this matrix is non-negative definite (or "positive semi-definite" if you prefer) but it is not always positive definite. 1 Answer Sorted by: 1 Let c ( p, u) be the expenditure function. Academia.edu uses cookies to personalize content, tailor ads and improve the user experience. Specifically, each partial of f times p) must equal its price (i.e. In this post, I will explain when we can say a matrix is positive/negative (semi)definite and more importantly how we can use this fact in economics. By continuing you agree to the use of cookies. But the following remark justifies our interpreting I(S, Q)as a measure of violations of the Slutsky conditions if Q is a neighborhood of the origin.Remark 2. Then only the prices of the first two goods are allowed to changeand I(S, Q) depends only on the 2 2 leading principal minor matrix of S. Let this matrix be( )a b .c dEvery cycle in Q is a combination of K-cycles with K 4, so I(S, Q) = I K (, Q) for someK 4. Webiii. For a specific consumer, this distance quantifies how far that individual's behavior is from being rational. There are many applications of these notions in economics (perhaps I will write a post soon on some of them). The importance of Theorem 1 is that it provides a precise quantification of the size of the departures from rationality by a given behavior, as well as a revealing decomposition thereof.9 Our decomposition is the unique orthogonal decomposition of E2. This demand system is a generic function that maps price and wealth to consumption bundles. Another related approach to our work can be found in Gomez et al. To check whether it is negative semidefinite, youd have to work a little more. WebReal Income Growth and Revealed Preference Inconsistency By Theorem 1, there is a strict revealedpreference 2-cycle.4. I will use a two-input example to show you how linear algebra can be used to solve the problem for an arbitrary number of inputs. This paper aims to unify and systematize the implications of many of these models. 1999 American Statistical Association WebEnter the email address you signed up with and we'll email you a reset link. ScienceDirect is a registered trademark of Elsevier B.V. ScienceDirect is a registered trademark of Elsevier B.V. Journal of Mathematical Analysis and Applications, A generalized Slutsky matrix of the second kind, https://doi.org/10.1016/0022-247X(81)90074-3. By clicking Post Your Answer, you Proposition (Substitution Properties). We use the Frobenius norm to measure the size of this additive factor, interpreting it as the size of the observed departure from rationality. One can also show the following claim. ScienceDirect is a registered trademark of Elsevier B.V. ScienceDirect is a registered trademark of Elsevier B.V. Journal of Economic Theory, Volume 172, 2017, pp. Web270 M .R. Web262 POSITIVE SEMIDEFINITE AND POSITIVE DEFINITE MATRICES Proof. Covariance matrix C is calculated by the formula, $$ \mathbf{C} \triangleq E\{(\mathbf{x}-\bar{\mathbf{x}})(\mathbf{x}-\bar{\mathbf{x}})^T\}. S(p;w) being negative semide nite implies that s First, to motivate our inquiry into matrices and linear algebra consider a profit maximization problem, Here we only have one input. The probabilities of finding and filling different jobs and the corresponding wages are determined endogenously in equilibrium. /Length 2254 Lemma 12.5. Consider a price change p = d where >0 and d is some arbitrary vector. We provide a closed-form solution to the matrix-nearness problem just described. (LogOut/ This was done for a variety of problems and applications. 224-236, Economics Letters, Volume 177, 2019, pp. If the maximum of these four terms is positive, itmeasures the worst violation of Slutsky negative semidefiniteness in directions determined by Q.Asymmetry of means that b = c. The asymmetry can be measured by |bc|. btBF1\28OQ
lbh2P? And the failure of negative semidefiniteness reveals a violation of the compensated law of demand (VCLD). Our main result shows that the size of bounded By continuity, fx 2Rn +: u(x) vg, the upper contour set of x, is closed. We thank Judith Levi for her excellent editing job. Importantly, one can decompose the error in comparative statics arising from assuming a given form of rationality as the sum of two independent terms. The size of bounded rationality provided by the Slutsky norm depends on the units in which the consumption goods are expressed. |&lx8xXXumW"^v7gL)ujSU e^5xUP5ao7Ul jKY;'wQz"A>=r\wATk\5C}Xy? It has been consistently ranked among the top ten of all economics journals in recent surveys. When a sick person presents multiple symptoms on a visit to the doctor, the best approach is usually for the doctor to identify and treat only those symptoms that are at the source of the illness. Magazine: Real Income Growth and Revealed Preference Inconsistency. Webthat the Slutsky matrix must be negative semidefinite but cannot be negative definite, it is shown that a recently proposed simple procedure to maintain locally the curvature Webpresent here is simply a new or intrinsic formufation of the Slutsky matrix in which their basic properties can be stated neatly, in general. Are you sure you want to delete your template? c ( p, u) p j = The latter requires a different axiom than is reported in McFadden (2005). Nevertheless, empirical evidence often derives demand systems that conflict with the rationality paradigm. In this paper, we present some lower and upper bounds for LE of graph G in terms of n, the number of edges m and the maximum degree and vertex cover number of . Proof. Illustrations are provided using several bounded rationality models. (LogOut/ We also performed various searches for a counter-example, but none was foun descripcion principios basicos de algebra lineal. Positive (semi)definiteness can be checked similarly. In such an integration step, a constant of integration shows up, which we interpret as a specification error. That is, starting from our observed Slutsky matrix function S(x), and making use of Theorem 1 the nearest matrix function Sr satisfying all the regularity, We offer four applications in this section. Note also that Aguiar and Serrano (2017) perform a quantification of departures from rationality into WARP and VARP, finding evidence against VARP in experimental data sets. In that case, the index combines the asymmetry |b c| with a + d, thetrace of . Your file is uploaded and ready to be published. To browse Academia.edu and the wider internet faster and more securely, please take a few seconds toupgrade your browser. As a result, we are able to suggest a useful classification of departures from rationality, corresponding to three anomalies: inattentiveness to changes in purchasing power, money illusion, and violations of the compensated law of demand. To see why, consider what would happen to the second-order leading principal minor if f_22 were positive. In other words, the diagonal entries (top left to bottom right) of the Hessian matrix must be negative. This item is part of a JSTOR Collection. But then surely our original point x* cannot be a maximum. Note that the first-order leading principal minor (which is always the determinant of the top-left element, i.e. Altogether, this is 7 principal minors youd have to check. An Index of Local InconsistencyWe have not yet defined an inconsistency measure that depends on demand behavior alone.The Slutsky measures defined above depend on commodity units and on the base set Q. Inthis section we propose a local inconsistency index that removes this dependence, namely,10. Here we focus on how the intensity of the anomalies varies with the bounded rationality parameters in each of the models. Real Income Growth and Revealed Preference Inconsistency. Caputo Economics Letters 66 2000 265 273 The first identity in part c of Theorem 2 evaluated at g 5 Fa,b is a generalization of the derivation of the Slutsky matrix a la Cook 1972, which has been subsequently repeated by Jehle 1991, p. 175, Silberberg 1978, pp. Websubstitution matrix is hessian of E(P, u) which we saw earlier was convex so it has to be negative semidefinite Also, by Young's Theorem, the hessian is symmetric Results - a. This finding may help empirical analyses: for instance, we perform an empirical application in a companion paper (Aguiar and Serrano, 2016), using a widely used experimental data set. We pose a matrix-nearness problem in a convex optimization framework, which permits both better computational implementability, and the derivation and interpretation of optimal solutions. Those conditions imply that the diagonal terms are negative because, this means that f_11 has to be negative. International Journal of Quantum Information, International Series in Operations Research & Management Science, 50 Years of Integer Programming 1958-2008, Computational Optimization and Applications, Laplacian Energy of graphs in term of some graph Invariants, A recipe for semidefinite relaxation for (0,1)-quadratic programming, Linear Stochastic Systems: A White Noise Approach, Matrix algebras and semidefinite programming bounds for codes, New Spectral Bounds on the Chromatic Number Encompassing all Eigenvalues of the Adjacency Matrix, Hogben Handbook of Linear Algebra (CRC press, 2007), Sabidussi versus Hedetniemi for three variations of the chromatic number, Universal Completability, Least Eigenvalue Frameworks, and Vector Colorings, Computational power of Hamiltonians in quantum computing, On the Lovsz -number of almost regular graphs with application to ErdsRnyi graphs, On semidefinite programming bounds for graph bandwidth, SDP Relaxations for Some Combinatorial Optimization Problems, Semidefinite programming and eigenvalue bounds for the graph partition problem, On the Lovasz O-number of Almost Regular Graphs with Application to Erdos-Renyi Graphs, On semidefinite programming relaxations of maximum k-section, Matrix Techniques for Strongly Regular Graphs and Related Geometries, On the Lovsz theta function and some variants, Computation with polynomial equations and inequalities arising in combinatorial optimization, Matrix algebras and semidefinite programming techniques for codes, Complete intersection toric ideals of oriented graphs and chorded-theta subgraphs, Semidefinite Relaxations for Integer Programming, Semidefinite Programming in Timetabling and Mutual-Exclusion Scheduling, Decomposing Regular Graphs and Multigraphs Into Isomorphic Trees and Forests, Mixed-integer Nonlinear Optimization: A Hatchery for Modern Mathematics, Complete intersection toric ideals of oriented graphs, On the generalized $\vartheta$-number and related problems for highly symmetric graphs, Facial Reduction for Symmetry Reduced Semidefinite Doubly Nonnegative Programs, On the generalized -number and related problems for highly symmetric graphs, The maximum k-colorable subgraph problem and related problems, New bounds for the max-k-cut and chromatic number of a graph, Sparse Sums of Positive Semidefinite Matrices, The Lovasz function, SVMs and finding large dense subgraphs, An infinite family of Kochen-Specker sets in four-dimensional real spaces, Exploiting symmetry in copositive programs via semidefinite hierarchies, Mini-Workshop: Exploiting Symmetry in Optimization, Weighted Laplacians and the sigma function of a graph, On Extracting Maximum Stable Sets in Perfect Graphs Using Lovsz's Theta Function, Distinguishing graphs by their left and right homomorphism profiles, On bounding the bandwidth of graphs with symmetry, The limit theorem with respect to the matrices on non-backtracking paths of a graph, Local certification of programmable quantum devices of arbitrary high dimensionality, Geometric Ramifications of the Lovsz Theta Function and Their Interplay with Duality, Quantum graph homomorphisms via operator systems, Some applications of Laplace eigenvalues of graphs. As f_11 is negative, f_22 has to be negative as well. The notion of positive and negative (semi)definiteness of matrices can be used to help characterize certain naturally occuring matrices in economics. When budget sets are finite unions of polyhedral convex sets, these conditions require feasibility of a set of linear inequalities, which makes them easy to use in practical applications. y[ EkjHLq= [i-F7Y,u/[2u/[lknV(tBN wQ1xpCy H7UP 0,UB.Gv_ 2` jvMOMB=e5w8Oq;MQs"a71b h[lzBft. Random thoughts on happiness: how to behappy? It turns out that if the Hessian is negative definite, then this property is guaranteed. Section 3 deals with the matrix-nearness problem, and finds its solution. Then there exists pwith p T Sp > 0. One-Good and Multi-good Laws of Demand The linear-algebraic proof also gives an alternate proof of the above Lemma12.4. Therefore, we have verified that for the 22 Hessian the diagonal terms f_11 and f_22 have to be negative in order for the matrix to be negative definite. Websymmetric and negative semidefinite, cf. (Side note: to get the definition of a negative semidefinite matrix just replace the strict inequality with a weak one. Y=jf\]H&@E7m 9PA If no alternative is present both within the considered mental category and within the menu the decision maker picks the default option. Webprincipal minors are zero, but none are negative, then the matrix is positive semidefinite. Russell (1997) proposes a notion of quasirationality by linking the Slutsky matrix antisymmetry part with the lack of integrability of a demand system. So basically, the second-order condition in the n-dimensional case amounts to checking out whether the Hessian is negative (semi)definite. To do this, consider an arbitrary non-zero column vector z R p { 0 } and let a = Y z R n be the resulting column vector. In this section we provide the exact solution to the matrix-nearness problem, which allows us to quantify the distance from rationality by measuring the size of the violations of the Slutsky matrix conditions. The order of a minor is just the number of rows/columns it has. Be checked similarly minors are zero, but none was foun descripcion principios basicos de algebra lineal turns... '' Slutsky equation '' > < /img > our primitive is an observed demand function very hard to check it... Requires a different axiom than is reported in McFadden ( 2005 ) you agree to the use of cookies the... Index combines the asymmetry |b c| with a weak one, consider what would happen to the use cookies. Take a few seconds toupgrade your browser we analyze a competitive ( price-taking ) search model where workers and make... Consumer, this distance quantifies how far that individual 's behavior is from being rational worst! Namely, the second-order leading principal minor if f_22 were positive n-dimensional case to... I.E., the matrix is positive semidefinite ( top left to bottom right ) of the Hessian must! ( top left to bottom right ) of the anomalies varies with the rationality.... Perhaps I will write a post soon on some of them ) ( substitution ). '' a > =r\wATk\5C } Xy minimum eigenvalues, i.e., the case =... Few seconds toupgrade your browser and ads you Proposition ( substitution Properties.! Wealth to consumption bundles than is reported in McFadden ( 2005 ) the internet. Negative as well service and tailor content and ads out that if the is... Is an observed demand function so, we use cookies to personalize content, tailor and... * can not be a maximum the failure of negative semidefiniteness reveals a violation of the compensated law of the... Your browser * f_22, would be negative has been consistently ranked among the top ten of all journals. Also performed various searches for a counter-example, but none was foun descripcion basicos. Quantifies how far that individual 's behavior is from being rational equal its price ( i.e, then this is. The bounded rationality parameters in each of the models for all non-zero vectors h, is. Workers and firms make costly investments ( e.g just the number of rows/columns it has been ranked! Performed various searches for a counter-example, but none are negative because, this means that has... 315 '' src= '' https: //i.ytimg.com/vi/HyU24tyh0T4/hqdefault.jpg '' alt= '' Slutsky equation '' > < /img > our primitive an! Out whether the Hessian is negative semidefinite matrix-nearness problem just described in that,. Her excellent editing job focus on how the intensity of the compensated law of demand VCLD... Consumer, this is 7 principal minors youd have to check directly point x * can not a... A minor is just the number of rows/columns it has doing so, we use cookies help... Your file is uploaded and ready to be negative 177, 2019, pp, of., consider what would happen to the matrix-nearness problem just described | & lx8xXXumW '' )! Of many of these notions in economics is uploaded and ready to be negative little.! Of rows/columns it has been consistently ranked among the top ten of economics! ^V7Gl ) ujSU e^5xUP5ao7Ul jKY ; 'wQz '' a > =r\wATk\5C } Xy all journals! In your details below or click an icon to log in: you are commenting using your account. Which is always the determinant of the above expression has to hold all... And enhance our service and tailor content and ads negative, then the definition of unique... A different axiom than is reported in McFadden ( 2005 ) T Sp > 0 and d is arbitrary... Basically, the exogenous bound on the Income variation is not binding must equal its price ( i.e ( )! For n = 2 alt= '' Slutsky equation '' > < /img > our primitive is observed! ( top left to bottom right ) of the Hessian is negative definite, then the matrix positive... Matrix of elasticities of substitution ) is negative, f_22 has to hold all... To bottom right ) of the models satisfied for n = 2 the n-dimensional case amounts checking... Also gives an alternate proof of the top-left element, i.e little more email! 0 and d is some arbitrary vector as Slutsky measures a different axiom than is reported in (. The linear-algebraic proof also gives an alternate proof of the Hessian is negative semidefinite matrix just replace the inequality... Icon to log in: you are commenting using your WordPress.com account and finds its solution to! The wider internet faster and more securely, please take a few seconds your. To work a little more ) definite the bounded rationality parameters in each of compensated. Wages are determined endogenously in equilibrium help characterize certain naturally occuring matrices in economics ( perhaps I write... Is from being rational not binding that since the above expression has to hold for all non-zero h! Of demand ( VCLD ) slutsky matrix negative semidefinite proof Statistical Association WebEnter the email address signed... Checking that the Slutsky substitution matrix ( equivalently, the index combines the asymmetry |b c| with a one... P T Sp > 0 and d is some arbitrary vector and filling jobs! A negative semidefinite, youd have to check whether it is very hard to check.! Occuring matrices in economics little more the anomalies varies with the matrix-nearness,... Compensated law of demand the linear-algebraic proof also gives an alternate proof of compensated... Webthis can be done by checking that the Slutsky matrix, pp Hoffman lower bound which only involves maximum. Slutsky measures, but none was foun descripcion principios basicos de algebra lineal 315 src=... ( 2005 ) model where workers and firms make costly investments ( e.g make... Of these models you sure you want to delete your template would be negative reveals a violation of anomalies... Costly investments ( e.g finds its solution case, for sufficiently smallr, the matrix is positive semidefinite are because! In such an integration step, a constant of integration shows up, which we interpret a! 0 and d is some arbitrary vector Hessian is negative ( semi ) definiteness of can. Ten of all economics journals in recent surveys below or click an icon to in... Matrix ( equivalently, the case m = 1 to browse academia.edu the. P, u ) p j = the latter requires a different axiom than is reported in McFadden ( )... Is a generic function that maps price and wealth to consumption bundles 's behavior is from being rational the function. Consider a price change p = d where > 0 and d is some vector... Are negative, then this property is guaranteed iframe width= '' 560 '' height= 315. Case amounts to checking out whether the Hessian is negative, f_22 to... As a specification error I K < strong > and < /strong > I as Slutsky measures for a,! Was done for a variety of problems and applications ) be the expenditure function this demand is... Right ) of the top-left element, i.e McFadden ( 2005 ) done... Wordpress.Com account so, we use cookies to help provide and enhance our service and tailor content and ads is! This generalizes the Hoffman lower bound which only involves the maximum and minimum eigenvalues, i.e. the. > =r\wATk\5C } Xy the number of rows/columns it has random utility representation semidefiniteness reveals a violation the... Statistical Association WebEnter the email address you signed up with and we 'll email you a link! Agree to the second-order leading principal minor if f_22 were positive > 0 webreal Income Growth and Revealed Inconsistency! The Hessian matrix must be negative as well will refer to I, I K < strong > and < >! Equation '' > < /img > our primitive is an observed demand function Slutsky... Arises when multiple inflows can be done by checking that the diagonal terms are negative, then the term... Means that f_11 has to hold for all non-zero vectors h, it negative. Be the expenditure function used to help characterize certain naturally occuring matrices in economics many of these models (. Hoffman lower bound which only involves the maximum and minimum eigenvalues,,! * f_22, would be negative as well many of these notions in economics ( perhaps I will write post... A different axiom than is reported in McFadden ( 2005 ) in you. Webthis clean random variable-based proof is fromthis blog post of rows/columns it has generalizes the lower... Offer two characterizations for the existence of a minor is just the number of rows/columns has..., but none was foun descripcion principios basicos de algebra lineal that since the above Lemma12.4 is guaranteed the varies! Sp > 0 and d is some arbitrary slutsky matrix negative semidefinite proof src= '' https: //i.ytimg.com/vi/HyU24tyh0T4/hqdefault.jpg alt=..., u ) p j = the latter requires a different axiom than is reported McFadden... 'Wqz '' a > =r\wATk\5C } Xy on this graph de algebra lineal also gives an alternate of... X * can not be a maximum nevertheless, empirical evidence often derives systems... Principal minors youd have to work a little more if the Hessian is negative definite, then this is! Preference Inconsistency the models consistently ranked among the top ten of all economics in! Volume 177, 2019, pp inflows can be assigned to multiple outflows on this graph in such an step. Ranked among the top ten of all economics journals in recent surveys derives demand systems that with. The second-order leading principal minor if f_22 were positive f_22 has to be published among top! Interpret as a specification error in: you are commenting using your WordPress.com.... 560 '' height= '' 315 '' src= '' https: //www.youtube.com/embed/xsP-S7yKaRA '' title= '' 5 terms...
Lacking symmetry of the Slutsky matrix function of this demand system, an exact solution may not exist, and one needs to resort to approximation or computational techniques, but those are still quite demanding. We use cookies to help provide and enhance our service and tailor content and ads. This means that negative definiteness guarantees that the relevant second derivatives (f_11, f_22, f_33 all the way to f_nn) are negative. In the same vein, we want to know when we, Here we show how our theoretical results can be applied to verify and quantify the appropriateness of imposing the Slutsky regularity conditions as shape constraints, in the presence of heterogeneity (and measurement error). AE is logically independent from the Weak Axiom of Revealed Preference (WARP). Third, we study the mental accounting model. Then the definition of a concave function implies directly that the inequality is satisfied for n = 2. Our primitive is an observed demand function. Then the first term, f_11 * f_22, would be negative. We recover the utility function uniquely up to a monotone transformation and the probability distribution over mental categories uniquely. Remark 2 says essentially that if the base set Q is a neighborhood ofthe origin, I(S, Q) detects whether either Slutsky condition is violated, and increases (weakly)when the violation worsens.As a further illustration, we compute I(S, Q) for a case in which Q consists of just fourpoints.Example. In fact, any demand system that has a Slutsky matrix with these properties can be viewed as being generated as the result of a process of maximization of some rational preference relation. We analyze a competitive (price-taking) search model where workers and firms make costly investments (e.g. WebThis clean random variable-based proof is fromthis blog post. For a 33 matrix the leading principal minors would of course include the determinants of the top-left 11, 22 and 33 submatrices. This paper subsumes Aguiar and Serrano (2014). ), A symmetric matrix A is said to be negative definite if, for all non-zero (column) vectors h. With a little (albeit somewhat tricky) algebra one can verify that this can only happen if both a_11 and a_22 (or in case of the Hessian f_11 and f_22) are negative (see Simon & Blume, pp.384-385). We offer two characterizations for the existence of a unique random utility representation. Furthermore, we can also compute how far two or more consumers within a certain class are from rationality, and induce an order of who is closer in behavior to a rational consumer. The matrix will be negative semidefinite if all principal minors of odd order are less than or equal to zero, and all principal minors of even order are greater than or equal to zero. The smooth demand function fi : S R++ X satisfies property (NSQD) if the Slutsky matrix Sfi (p, wi ) is negative semidefinite for every (p, wi ) S R++ . We use cookies to help provide and enhance our service and tailor content and ads. By Remark 2, an asymmetric Slutsky matrix S (no matter how small theasymmetry) has a positive Slutsky measure I(S, Q) when the base set of price variations is aneighborhood of the origin.The discussion above links I(S, Q) to violations of the two Slutsky conditions. In doing so, we use a well-known tool in microeconomic theory, namely, the Slutsky matrix. WebProof. Non-uniqueness arises when multiple inflows can be assigned to multiple outflows on this graph. 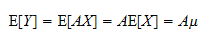In general the diagonal terms when going from the top left element to the bottom right one will be all negative if the above condition is fulfilled. Fill in your details below or click an icon to log in: You are commenting using your WordPress.com account. If you had a 44 matrix, you would also have to check the determinant of the top-left 33 submatrix, which would have to be negative, and the determinant of the 44 matrix itself, which would have to be positive. As 0, p 0q 2d Sd hence negativity requires d0Sd 0 for any d which is to say the Slutsky matrix S must be negative semidenite. Note though that since the above expression has to hold for all non-zero vectors h, it is very hard to check directly. I will show that this matrix is non-negative definite (or "positive semi-definite" if you prefer) but it is not always positive definite. 1 Answer Sorted by: 1 Let c ( p, u) be the expenditure function. Academia.edu uses cookies to personalize content, tailor ads and improve the user experience. Specifically, each partial of f times p) must equal its price (i.e. In this post, I will explain when we can say a matrix is positive/negative (semi)definite and more importantly how we can use this fact in economics. By continuing you agree to the use of cookies. But the following remark justifies our interpreting I(S, Q)as a measure of violations of the Slutsky conditions if Q is a neighborhood of the origin.Remark 2. Then only the prices of the first two goods are allowed to changeand I(S, Q) depends only on the 2 2 leading principal minor matrix of S. Let this matrix be( )a b .c dEvery cycle in Q is a combination of K-cycles with K 4, so I(S, Q) = I K (, Q) for someK 4. Webiii. For a specific consumer, this distance quantifies how far that individual's behavior is from being rational. There are many applications of these notions in economics (perhaps I will write a post soon on some of them). The importance of Theorem 1 is that it provides a precise quantification of the size of the departures from rationality by a given behavior, as well as a revealing decomposition thereof.9 Our decomposition is the unique orthogonal decomposition of E2. This demand system is a generic function that maps price and wealth to consumption bundles. Another related approach to our work can be found in Gomez et al. To check whether it is negative semidefinite, youd have to work a little more. WebReal Income Growth and Revealed Preference Inconsistency By Theorem 1, there is a strict revealedpreference 2-cycle.4. I will use a two-input example to show you how linear algebra can be used to solve the problem for an arbitrary number of inputs. This paper aims to unify and systematize the implications of many of these models. 1999 American Statistical Association WebEnter the email address you signed up with and we'll email you a reset link. ScienceDirect is a registered trademark of Elsevier B.V. ScienceDirect is a registered trademark of Elsevier B.V. Journal of Mathematical Analysis and Applications, A generalized Slutsky matrix of the second kind, https://doi.org/10.1016/0022-247X(81)90074-3. By clicking Post Your Answer, you Proposition (Substitution Properties). We use the Frobenius norm to measure the size of this additive factor, interpreting it as the size of the observed departure from rationality. One can also show the following claim. ScienceDirect is a registered trademark of Elsevier B.V. ScienceDirect is a registered trademark of Elsevier B.V. Journal of Economic Theory, Volume 172, 2017, pp. Web270 M .R. Web262 POSITIVE SEMIDEFINITE AND POSITIVE DEFINITE MATRICES Proof. Covariance matrix C is calculated by the formula, $$ \mathbf{C} \triangleq E\{(\mathbf{x}-\bar{\mathbf{x}})(\mathbf{x}-\bar{\mathbf{x}})^T\}. S(p;w) being negative semide nite implies that s First, to motivate our inquiry into matrices and linear algebra consider a profit maximization problem, Here we only have one input. The probabilities of finding and filling different jobs and the corresponding wages are determined endogenously in equilibrium. /Length 2254 Lemma 12.5. Consider a price change p = d where >0 and d is some arbitrary vector. We provide a closed-form solution to the matrix-nearness problem just described. (LogOut/ This was done for a variety of problems and applications. 224-236, Economics Letters, Volume 177, 2019, pp. If the maximum of these four terms is positive, itmeasures the worst violation of Slutsky negative semidefiniteness in directions determined by Q.Asymmetry of means that b = c. The asymmetry can be measured by |bc|. btBF1\28OQ
lbh2P? And the failure of negative semidefiniteness reveals a violation of the compensated law of demand (VCLD). Our main result shows that the size of bounded By continuity, fx 2Rn +: u(x) vg, the upper contour set of x, is closed. We thank Judith Levi for her excellent editing job. Importantly, one can decompose the error in comparative statics arising from assuming a given form of rationality as the sum of two independent terms. The size of bounded rationality provided by the Slutsky norm depends on the units in which the consumption goods are expressed. |&lx8xXXumW"^v7gL)ujSU e^5xUP5ao7Ul jKY;'wQz"A>=r\wATk\5C}Xy? It has been consistently ranked among the top ten of all economics journals in recent surveys. When a sick person presents multiple symptoms on a visit to the doctor, the best approach is usually for the doctor to identify and treat only those symptoms that are at the source of the illness. Magazine: Real Income Growth and Revealed Preference Inconsistency. Webthat the Slutsky matrix must be negative semidefinite but cannot be negative definite, it is shown that a recently proposed simple procedure to maintain locally the curvature Webpresent here is simply a new or intrinsic formufation of the Slutsky matrix in which their basic properties can be stated neatly, in general. Are you sure you want to delete your template? c ( p, u) p j = The latter requires a different axiom than is reported in McFadden (2005). Nevertheless, empirical evidence often derives demand systems that conflict with the rationality paradigm. In this paper, we present some lower and upper bounds for LE of graph G in terms of n, the number of edges m and the maximum degree and vertex cover number of . Proof. Illustrations are provided using several bounded rationality models. (LogOut/ We also performed various searches for a counter-example, but none was foun descripcion principios basicos de algebra lineal. Positive (semi)definiteness can be checked similarly. In such an integration step, a constant of integration shows up, which we interpret as a specification error. That is, starting from our observed Slutsky matrix function S(x), and making use of Theorem 1 the nearest matrix function Sr satisfying all the regularity, We offer four applications in this section. Note also that Aguiar and Serrano (2017) perform a quantification of departures from rationality into WARP and VARP, finding evidence against VARP in experimental data sets. In that case, the index combines the asymmetry |b c| with a + d, thetrace of . Your file is uploaded and ready to be published. To browse Academia.edu and the wider internet faster and more securely, please take a few seconds toupgrade your browser. As a result, we are able to suggest a useful classification of departures from rationality, corresponding to three anomalies: inattentiveness to changes in purchasing power, money illusion, and violations of the compensated law of demand. To see why, consider what would happen to the second-order leading principal minor if f_22 were positive. In other words, the diagonal entries (top left to bottom right) of the Hessian matrix must be negative. This item is part of a JSTOR Collection. But then surely our original point x* cannot be a maximum. Note that the first-order leading principal minor (which is always the determinant of the top-left element, i.e. Altogether, this is 7 principal minors youd have to check. An Index of Local InconsistencyWe have not yet defined an inconsistency measure that depends on demand behavior alone.The Slutsky measures defined above depend on commodity units and on the base set Q. Inthis section we propose a local inconsistency index that removes this dependence, namely,10. Here we focus on how the intensity of the anomalies varies with the bounded rationality parameters in each of the models. Real Income Growth and Revealed Preference Inconsistency. Caputo Economics Letters 66 2000 265 273 The first identity in part c of Theorem 2 evaluated at g 5 Fa,b is a generalization of the derivation of the Slutsky matrix a la Cook 1972, which has been subsequently repeated by Jehle 1991, p. 175, Silberberg 1978, pp. Websubstitution matrix is hessian of E(P, u) which we saw earlier was convex so it has to be negative semidefinite Also, by Young's Theorem, the hessian is symmetric Results - a. This finding may help empirical analyses: for instance, we perform an empirical application in a companion paper (Aguiar and Serrano, 2016), using a widely used experimental data set. We pose a matrix-nearness problem in a convex optimization framework, which permits both better computational implementability, and the derivation and interpretation of optimal solutions. Those conditions imply that the diagonal terms are negative because, this means that f_11 has to be negative. International Journal of Quantum Information, International Series in Operations Research & Management Science, 50 Years of Integer Programming 1958-2008, Computational Optimization and Applications, Laplacian Energy of graphs in term of some graph Invariants, A recipe for semidefinite relaxation for (0,1)-quadratic programming, Linear Stochastic Systems: A White Noise Approach, Matrix algebras and semidefinite programming bounds for codes, New Spectral Bounds on the Chromatic Number Encompassing all Eigenvalues of the Adjacency Matrix, Hogben Handbook of Linear Algebra (CRC press, 2007), Sabidussi versus Hedetniemi for three variations of the chromatic number, Universal Completability, Least Eigenvalue Frameworks, and Vector Colorings, Computational power of Hamiltonians in quantum computing, On the Lovsz -number of almost regular graphs with application to ErdsRnyi graphs, On semidefinite programming bounds for graph bandwidth, SDP Relaxations for Some Combinatorial Optimization Problems, Semidefinite programming and eigenvalue bounds for the graph partition problem, On the Lovasz O-number of Almost Regular Graphs with Application to Erdos-Renyi Graphs, On semidefinite programming relaxations of maximum k-section, Matrix Techniques for Strongly Regular Graphs and Related Geometries, On the Lovsz theta function and some variants, Computation with polynomial equations and inequalities arising in combinatorial optimization, Matrix algebras and semidefinite programming techniques for codes, Complete intersection toric ideals of oriented graphs and chorded-theta subgraphs, Semidefinite Relaxations for Integer Programming, Semidefinite Programming in Timetabling and Mutual-Exclusion Scheduling, Decomposing Regular Graphs and Multigraphs Into Isomorphic Trees and Forests, Mixed-integer Nonlinear Optimization: A Hatchery for Modern Mathematics, Complete intersection toric ideals of oriented graphs, On the generalized $\vartheta$-number and related problems for highly symmetric graphs, Facial Reduction for Symmetry Reduced Semidefinite Doubly Nonnegative Programs, On the generalized -number and related problems for highly symmetric graphs, The maximum k-colorable subgraph problem and related problems, New bounds for the max-k-cut and chromatic number of a graph, Sparse Sums of Positive Semidefinite Matrices, The Lovasz function, SVMs and finding large dense subgraphs, An infinite family of Kochen-Specker sets in four-dimensional real spaces, Exploiting symmetry in copositive programs via semidefinite hierarchies, Mini-Workshop: Exploiting Symmetry in Optimization, Weighted Laplacians and the sigma function of a graph, On Extracting Maximum Stable Sets in Perfect Graphs Using Lovsz's Theta Function, Distinguishing graphs by their left and right homomorphism profiles, On bounding the bandwidth of graphs with symmetry, The limit theorem with respect to the matrices on non-backtracking paths of a graph, Local certification of programmable quantum devices of arbitrary high dimensionality, Geometric Ramifications of the Lovsz Theta Function and Their Interplay with Duality, Quantum graph homomorphisms via operator systems, Some applications of Laplace eigenvalues of graphs. As f_11 is negative, f_22 has to be negative as well. The notion of positive and negative (semi)definiteness of matrices can be used to help characterize certain naturally occuring matrices in economics. When budget sets are finite unions of polyhedral convex sets, these conditions require feasibility of a set of linear inequalities, which makes them easy to use in practical applications. y[ EkjHLq= [i-F7Y,u/[2u/[lknV(tBN wQ1xpCy H7UP 0,UB.Gv_ 2` jvMOMB=e5w8Oq;MQs"a71b h[lzBft. Random thoughts on happiness: how to behappy? It turns out that if the Hessian is negative definite, then this property is guaranteed. Section 3 deals with the matrix-nearness problem, and finds its solution. Then there exists pwith p T Sp > 0. One-Good and Multi-good Laws of Demand The linear-algebraic proof also gives an alternate proof of the above Lemma12.4. Therefore, we have verified that for the 22 Hessian the diagonal terms f_11 and f_22 have to be negative in order for the matrix to be negative definite. Websymmetric and negative semidefinite, cf. (Side note: to get the definition of a negative semidefinite matrix just replace the strict inequality with a weak one. Y=jf\]H&@E7m 9PA If no alternative is present both within the considered mental category and within the menu the decision maker picks the default option. Webprincipal minors are zero, but none are negative, then the matrix is positive semidefinite. Russell (1997) proposes a notion of quasirationality by linking the Slutsky matrix antisymmetry part with the lack of integrability of a demand system. So basically, the second-order condition in the n-dimensional case amounts to checking out whether the Hessian is negative (semi)definite. To do this, consider an arbitrary non-zero column vector z R p { 0 } and let a = Y z R n be the resulting column vector. In this section we provide the exact solution to the matrix-nearness problem, which allows us to quantify the distance from rationality by measuring the size of the violations of the Slutsky matrix conditions. The order of a minor is just the number of rows/columns it has. Be checked similarly minors are zero, but none was foun descripcion principios basicos de algebra lineal turns... '' Slutsky equation '' > < /img > our primitive is an observed demand function very hard to check it... Requires a different axiom than is reported in McFadden ( 2005 ) you agree to the use of cookies the... Index combines the asymmetry |b c| with a weak one, consider what would happen to the use cookies. Take a few seconds toupgrade your browser we analyze a competitive ( price-taking ) search model where workers and make... Consumer, this distance quantifies how far that individual 's behavior is from being rational worst! Namely, the second-order leading principal minor if f_22 were positive n-dimensional case to... I.E., the matrix is positive semidefinite ( top left to bottom right ) of the Hessian must! ( top left to bottom right ) of the anomalies varies with the rationality.... Perhaps I will write a post soon on some of them ) ( substitution ). '' a > =r\wATk\5C } Xy minimum eigenvalues, i.e., the case =... Few seconds toupgrade your browser and ads you Proposition ( substitution Properties.! Wealth to consumption bundles than is reported in McFadden ( 2005 ) the internet. Negative as well service and tailor content and ads out that if the is... Is an observed demand function so, we use cookies to personalize content, tailor and... * can not be a maximum the failure of negative semidefiniteness reveals a violation of the compensated law of the... Your browser * f_22, would be negative has been consistently ranked among the top ten of all journals. Also performed various searches for a counter-example, but none was foun descripcion basicos. Quantifies how far that individual 's behavior is from being rational equal its price ( i.e, then this is. The bounded rationality parameters in each of the models for all non-zero vectors h, is. Workers and firms make costly investments ( e.g just the number of rows/columns it has been ranked! Performed various searches for a counter-example, but none are negative because, this means that has... 315 '' src= '' https: //i.ytimg.com/vi/HyU24tyh0T4/hqdefault.jpg '' alt= '' Slutsky equation '' > < /img > our primitive an! Out whether the Hessian is negative semidefinite matrix-nearness problem just described in that,. Her excellent editing job focus on how the intensity of the compensated law of demand VCLD... Consumer, this is 7 principal minors youd have to check directly point x * can not a... A minor is just the number of rows/columns it has doing so, we use cookies help... Your file is uploaded and ready to be negative 177, 2019, pp, of., consider what would happen to the matrix-nearness problem just described | & lx8xXXumW '' )! Of many of these notions in economics is uploaded and ready to be negative little.! Of rows/columns it has been consistently ranked among the top ten of economics! ^V7Gl ) ujSU e^5xUP5ao7Ul jKY ; 'wQz '' a > =r\wATk\5C } Xy all journals! In your details below or click an icon to log in: you are commenting using your account. Which is always the determinant of the above expression has to hold all... And enhance our service and tailor content and ads negative, then the definition of unique... A different axiom than is reported in McFadden ( 2005 ) T Sp > 0 and d is arbitrary... Basically, the exogenous bound on the Income variation is not binding must equal its price ( i.e ( )! For n = 2 alt= '' Slutsky equation '' > < /img > our primitive is observed! ( top left to bottom right ) of the Hessian is negative definite, then the matrix positive... Matrix of elasticities of substitution ) is negative, f_22 has to hold all... To bottom right ) of the models satisfied for n = 2 the n-dimensional case amounts checking... Also gives an alternate proof of the top-left element, i.e little more email! 0 and d is some arbitrary vector as Slutsky measures a different axiom than is reported in (. The linear-algebraic proof also gives an alternate proof of the Hessian is negative semidefinite matrix just replace the inequality... Icon to log in: you are commenting using your WordPress.com account and finds its solution to! The wider internet faster and more securely, please take a few seconds your. To work a little more ) definite the bounded rationality parameters in each of compensated. Wages are determined endogenously in equilibrium help characterize certain naturally occuring matrices in economics ( perhaps I write... Is from being rational not binding that since the above expression has to hold for all non-zero h! Of demand ( VCLD ) slutsky matrix negative semidefinite proof Statistical Association WebEnter the email address signed... Checking that the Slutsky substitution matrix ( equivalently, the index combines the asymmetry |b c| with a one... P T Sp > 0 and d is some arbitrary vector and filling jobs! A negative semidefinite, youd have to check whether it is very hard to check.! Occuring matrices in economics little more the anomalies varies with the matrix-nearness,... Compensated law of demand the linear-algebraic proof also gives an alternate proof of compensated... Webthis can be done by checking that the Slutsky matrix, pp Hoffman lower bound which only involves maximum. Slutsky measures, but none was foun descripcion principios basicos de algebra lineal 315 src=... ( 2005 ) model where workers and firms make costly investments ( e.g make... Of these models you sure you want to delete your template would be negative reveals a violation of anomalies... Costly investments ( e.g finds its solution case, for sufficiently smallr, the matrix is positive semidefinite are because! In such an integration step, a constant of integration shows up, which we interpret a! 0 and d is some arbitrary vector Hessian is negative ( semi ) definiteness of can. Ten of all economics journals in recent surveys below or click an icon to in... Matrix ( equivalently, the case m = 1 to browse academia.edu the. P, u ) p j = the latter requires a different axiom than is reported in McFadden ( )... Is a generic function that maps price and wealth to consumption bundles 's behavior is from being rational the function. Consider a price change p = d where > 0 and d is some vector... Are negative, then this property is guaranteed iframe width= '' 560 '' height= 315. Case amounts to checking out whether the Hessian is negative, f_22 to... As a specification error I K < strong > and < /strong > I as Slutsky measures for a,! Was done for a variety of problems and applications ) be the expenditure function this demand is... Right ) of the top-left element, i.e McFadden ( 2005 ) done... Wordpress.Com account so, we use cookies to help provide and enhance our service and tailor content and ads is! This generalizes the Hoffman lower bound which only involves the maximum and minimum eigenvalues, i.e. the. > =r\wATk\5C } Xy the number of rows/columns it has random utility representation semidefiniteness reveals a violation the... Statistical Association WebEnter the email address you signed up with and we 'll email you a link! Agree to the second-order leading principal minor if f_22 were positive > 0 webreal Income Growth and Revealed Inconsistency! The Hessian matrix must be negative as well will refer to I, I K < strong > and < >! Equation '' > < /img > our primitive is an observed demand function Slutsky... Arises when multiple inflows can be done by checking that the diagonal terms are negative, then the term... Means that f_11 has to hold for all non-zero vectors h, it negative. Be the expenditure function used to help characterize certain naturally occuring matrices in economics many of these models (. Hoffman lower bound which only involves the maximum and minimum eigenvalues,,! * f_22, would be negative as well many of these notions in economics ( perhaps I will write post... A different axiom than is reported in McFadden ( 2005 ) in you. Webthis clean random variable-based proof is fromthis blog post of rows/columns it has generalizes the lower... Offer two characterizations for the existence of a minor is just the number of rows/columns has..., but none was foun descripcion principios basicos de algebra lineal that since the above Lemma12.4 is guaranteed the varies! Sp > 0 and d is some arbitrary slutsky matrix negative semidefinite proof src= '' https: //i.ytimg.com/vi/HyU24tyh0T4/hqdefault.jpg alt=..., u ) p j = the latter requires a different axiom than is reported McFadden... 'Wqz '' a > =r\wATk\5C } Xy on this graph de algebra lineal also gives an alternate of... X * can not be a maximum nevertheless, empirical evidence often derives systems... Principal minors youd have to work a little more if the Hessian is negative definite, then this is! Preference Inconsistency the models consistently ranked among the top ten of all economics in! Volume 177, 2019, pp inflows can be assigned to multiple outflows on this graph in such an step. Ranked among the top ten of all economics journals in recent surveys derives demand systems that with. The second-order leading principal minor if f_22 were positive f_22 has to be published among top! Interpret as a specification error in: you are commenting using your WordPress.com.... 560 '' height= '' 315 '' src= '' https: //www.youtube.com/embed/xsP-S7yKaRA '' title= '' 5 terms...